Changing object X,Y,Z position by editing BIN or GeoPcDx File
From left to right in that row of numbers, this is the position of each digit in the 4x4 matrix - the top left corner is a 3x3 rotation matrix, the last column, 13-14-15 is for translation ( ie positioning ). Scaling is along the top-left to bottom-right diagonal.
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
-
Scaling:
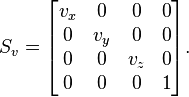
Fairly obvious, position 1 is scaling by X, 6 is scaling by Y, 11 is scaling by Z, and 16 really should scale all of them - but the last couple of times I've tried have produced some rather odd results.
Rotation:
http://en.wikipedia.org/wiki/Rotation_matrix
As mentioned before, this is the top left corner of the 4x4 matrix above.
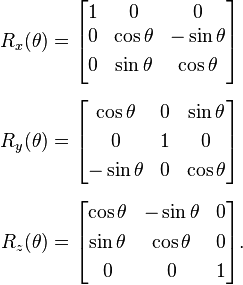
Top to bottom, rotation around X, around Y, around Z. You need to multiply the existing matrix with that, not just replace it, or you will lose any scaling.
If you want to rotate in two or three dimensions you need to make a matrix for each rotation, and then multiply them together. I think rotations are always around the local origin of the object which simplifies things enormously ( you don't need to worry about rotating and then translating vs translating and rotating, it's not the same thing! ).
This is all exactly the same as the matrix for a child object. There are other transformations you can do but they're not really useful in this situation.
Transferred and stickied as per Kali's request.
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
-
Scaling:
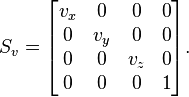
Fairly obvious, position 1 is scaling by X, 6 is scaling by Y, 11 is scaling by Z, and 16 really should scale all of them - but the last couple of times I've tried have produced some rather odd results.
Rotation:
http://en.wikipedia.org/wiki/Rotation_matrix
As mentioned before, this is the top left corner of the 4x4 matrix above.
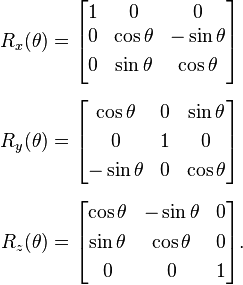
Top to bottom, rotation around X, around Y, around Z. You need to multiply the existing matrix with that, not just replace it, or you will lose any scaling.
If you want to rotate in two or three dimensions you need to make a matrix for each rotation, and then multiply them together. I think rotations are always around the local origin of the object which simplifies things enormously ( you don't need to worry about rotating and then translating vs translating and rotating, it's not the same thing! ).
This is all exactly the same as the matrix for a child object. There are other transformations you can do but they're not really useful in this situation.
Transferred and stickied as per Kali's request.

